
Problème n°7
Etudier si les courbes respectives des fonctions ln et exp admettent des
tangentes communes et si oui lesquelles.

Soit (d) une droite tangente aux deux courbes en A(a,ln(a)) et B(b,eb).
(avec a >0)
La pente de (d) est à la fois 1/a et eb. Donc eb = 1/a ou
encore a = e-b
L'ordonnée à l'origine de (d) est à la fois eb-beb
= (1-b)eb et ln(a) - 1. Donc (1-b)eb = ln(a) -
1
Par substitution on obtient : (1-b)eb = ln(e-b) - 1
ou encore (1-b)eb + b + 1 = 0 ou encore eb = (b +
1)/ (b-1) (b=1 ne convient pas)
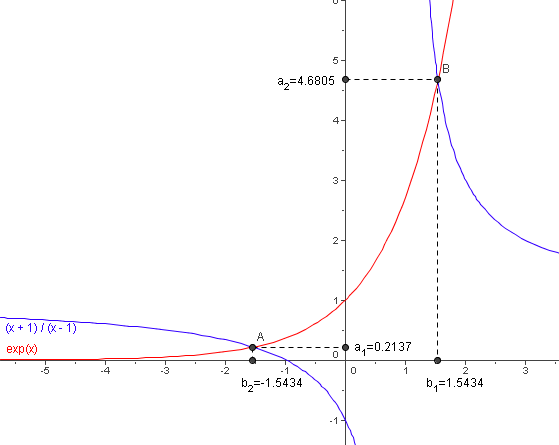
Il suffit donc de tracer les deux courbes y=ex et y=(x + 1)/ (x-1) et
trouver leurs intersections.
| L'étude et le graphique des deux fonctions montrent qu'il y
a deux solutions b1 et b2 et il semble qu'elles
soient opposées: b2 = -b1. Supposons que b soit une solution, montrons alors que -b est aussi solution de ex = (x + 1)/ (x-1): On a donc eb = (b + 1)/ (b-1), e-b = 1/eb = (b - 1)/ (b+1) et (-b + 1)/ (-b-1) = (b - 1)/ (b+1) on a donc bien -b solution de ex = (x + 1)/ (x-1). La calculatrice ou un tableur permettent de donner une valeur
approchée de b1: b1 »
1,5434. Il y a donc deux droites (d1) et (d2) tangentes
aux deux courbes de l'exponentielle et du logarithme: |
 |
Prolongements:
1) On peut construire une suite convergeant vers b1:
On veut trouver la solution positive de l'équation ex-(x+1)/(x-1) =
0.
Méthode des tangentes: U0=1,5, Bn est le point de
la courbe représentant la fonction f définie par f(x) = ex-(x+1)/(x-1)
d'abscisse Un. La tangente en Bn à la courbe coupe l'axe
des abscisses au point d'abscisse Un+1. Montrer que la suite U
converge vers b1.
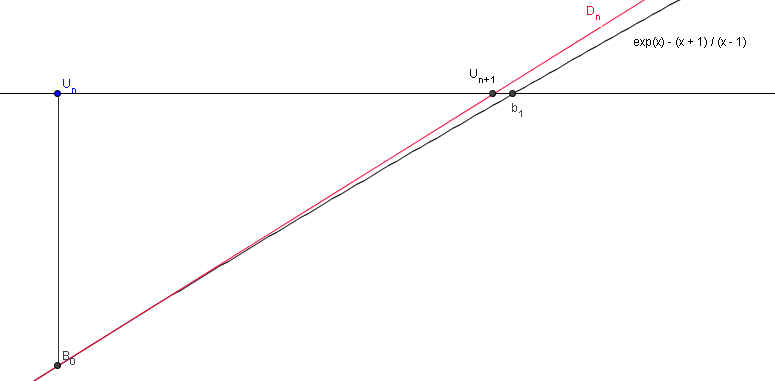
Équation de la tangente en Bn: y = f (Un) + (x-Un)
f ' (Un).
Un+1 = Un - f (Un) / f '
(Un) avec f ' (x) = ex + 2 / (x-1)²
et f(x) = ex-(x+1)/(x-1) ...
sur Excel :
| n | U | f (U) | f ' (U) |
| 0 | 1,5 | -0,51831093 | 12,4816891 |
| 1 | 1,5415257 | -0,02155633 | 11,4918298 |
| 2 | 1,5434015 | -3,5937E-05 | 11,453597 |
| 3 | 1,54340464 | -9,9666E-11 | 11,4535335 |
| 4 | 1,54340464 | 0 | 11,4535335 |
| 5 | 1,54340464 | 0 | 11,4535335 |
2) Les deux tangentes trouvées sont symétriques par
rapport à la droite d'équation y=x (dans un repère orthonormé).